Hoofdstuk 2 DATA, HUN VOORSTELLING EN DE LUKRAKE STEEKPROEF
2.1 SOORTEN DATA
Variabelen worden ingedeeld naargelang hun meetniveau, afhankelijk van de schaal waarop ze worden gemeten. Nominale en ordinale variabelen zijn zogenaamde categorische of kwalitatieve variabelen. Daarnaast zijn er ook nog kwantitatieve variabelen.
2.1.1 NOMINALE VARIABELEN
Met behulp van een nominale variabele kunnen de elementen van een steekproef of van een populatie geclassificeerd worden: de waarde van de variabele plaatst een element in een bepaalde klasse of categorie. Voorbeelden van dergelijke variabelen zijn.
- geslacht (man/vrouw),
- nationaliteit (Belg/Nederlander/. . . ),
- godsdienst (katholiek/protestants/. . . ),
- het al dan niet bezitten van een wagen (ja/neen).
Soms kan het nuttig zijn labels, codenummers of -letters toe te kennen aan de verschillende klassen of categorieën. Zo kan een Belg de code ”1” krijgen, een Nederlander de code ”2”, een Fransman de code ”3”, en een Duitser de code ”4”. Belangrijk hierbij is op te merken dat deze cijfers geen volgorde en/of hoeveelheid impliceren. Daarom zijn, behalve het berekenen van percentages, de meeste rekenkundige bewerkingen op nominale variabelen zinloos. Deze krijgen dan ook maar weinig aandacht in deze inleidende cursus (hoewel er heel wat statistische methodes voor dit type van data beschikbaar zijn).
2.1.2 ORDINALE VARIABELEN
Indien een nominale variabele een logische ordening tussen de elementen van een steekproef toelaat, dan is de variabele ordinaal. Een typisch voorbeeld van een ordinale variabele wordt aangetroffen in allerhande enquêtes. Daar wordt de respondenten vaak gevraagd of zij de kwaliteit van een product of dienst als ”1: zeer goed”, ”2: goed”, ”3: matig”, ”4: slecht” of ”5: zeer slecht” zouden bestempelen. In andere enquêtes wordt de respondenten gevraagd of zij het ”1: helemaal eens”, ”2: eerder eens”, ”3: noch eens, noch oneens”, ”4: eerder oneens” of ”5: helemaal oneens” zijn met een bepaalde stelling. Ander voorbeelden van ordinale variabelen zijn het aantal Michelin-sterren van restaurants of het aantal sterren van hotels. Een ordinale schaal heeft geen vaste meeteenheid, dit wil zeggen dat het verschil tussen de verschillende niveaus op de meetschaal niet in een aantal eenheden kan uitgedrukt worden. Het verschil tussen een hotel met drie sterren en één met twee sterren is bijvoorbeeld niet noodzakelijk hetzelfde als het verschil tussen een hotel met twee sterren en één met slechts één enkele ster. Het spreekt vanzelf dat het ook bij ordinale variabelen weinig zinvol is rekenkundige bewerkingen uit te voeren, zoals het berekenen van een gemiddelde, en er zal dan ook weinig gebruik van gemaakt worden in deze cursus.
2.1.3 KWANTITATIEVE VARIABELEN
Een variabele die gemeten wordt op een kwantitatieve schaal kan uitgedrukt worden in een aantal vaste meeteenheden. Voorbeelden zijn lengte, oppervlakte, inhoud, gewicht, duurtijd, aantal bits per tijdseenheid, prijs, inkomen, wachttijd, aantal bestelde goederen. . . . Op kwantitatieve variabelen kunnen vrijwel alle rekenkundige bewerkingen zinvol worden uitgevoerd. Het verschil tussen verschillende waarden van een variabele kan, in tegenstelling tot bij een ordinale variabele, in een aantal eenheden uitgedrukt worden. Binnen de kwantitatieve variabelen wordt nog een onderscheid gemaakt tussen variabelen die gemeten worden op een intervalschaal en variabelen die op een ratioschaal gemeten worden. Er wordt tevens een onderscheid gemaakt tussen discrete en continue variabelen.
Intervalschaal: Een intervalschaal heeft geen natuurlijk nulpunt. Bij variabelen gemeten op een intervalschaal kunnen verhoudingen niet zinvol berekend worden. Bekende voorbeelden van intervalvariabelen zijn de tijd afgelezen op een klok en de temperatuur uitgedrukt in graden Celsius of Fahrenheit. Het verschil tussen 2 uur en 4 uur is hetzelfde als het verschil tussen 21 uur en 23 uur, maar het is niet zo dat 4 uur twee keer zo laat is als 2 uur. Dit is te wijten aan het feit dat de tijd afgelezen op een klok geen absoluut nulpunt heeft (voor een tijdsaanduiding met een absoluut nulpunt verwijzen we naar de Juliaanse Dag, deze is ook op elk moment hetzelfde over de hele wereld). Hetzelfde geldt voor de temperatuur gemeten in graden Celsius: 20 graden Celsius is niet vier keer zo warm als 5 graden Celsius, het is 15 graden Celsius warmer.
Ratioschaal: Een ratioschaal heeft wel een absoluut nulpunt. Verhoudingen kunnen daarom bij gegevens die gemeten worden op een ratioschaal zinvol berekend worden. Een lengte van 6 cm is dubbel zoveel als een lengte van 3 cm omdat de lengteschaal een absoluut nulpunt heeft. Analoog is een bestelling van 6 producten dubbel zo groot als een order van 3 producten. Ook temperatuur in Kelvin wordt gemeten op een ratioschaal, want 10 Kelvin is dubbel zo warm in vergelijking met 5 Kelvin.
Discrete versus continue variabelen: Een discrete variabele kan slechts een eindig of oneindig aftelbaar aantal verschillende waarden aannemen, terwijl een continue variabele een continuüm van waarden kan aannemen. Voorbeelden van discrete variabelen zijn het aantal passagiers op een lijnvlucht, het aantal kinderen in een gezin of het aantal verzekeringspolissen dat een gezin afsloot. Voorbeelden van continue variabelen zijn lengte, duurtijd, gewicht en body mass index. In de praktijk zullen alle waarnemingen van een continue variabele discreet zijn: een continue lengte wordt in de praktijk gemeten tot op een bepaalde nauwkeurigheid (bijvoorbeeld een millimeter) en aldus discreet gemaakt. Toch zullen we die lengte dan bestuderen alsof het een continue variabele betrof.
2.1.4 HIËRARCHIE VAN MEETSCHALEN
Uit het bovenstaande blijkt duidelijk dat er een hiërarchie zit in de meetschalen. De hoogste of meest informatieve meetschaal is de ratioschaal, gevolg door de intervalschaal, en de ordinale en nominale meetschalen. Gegevens die op een bepaalde schaal gemeten worden, kunnen daarom omgevormd worden tot gegevens van een lagere meetschaal. Gegevens gemeten op een ratioschaal (bijvoorbeeld lengte) zijn natuurlijk interval geschaald (het verschil tussen 6 cm en 3 cm is hetzelfde als het verschil tussen 15 cm en 12 cm), ordinaal (lengtes kunnen zinvol geordend worden) en nominaal (lengtes kunnen ingedeeld worden in klassen). Omgekeerd kunnen nominale gegevens nooit omgevormd worden tot ordinale of kwantitatieve gegevens. Daarom zullen in het vervolg van de cursus alle technieken die toepasbaar zijn op nominale gegevens, automatisch toepasbaar zijn op ordinale en kwantitatieve gegevens. Alle technieken die toepasbaar zijn op ordinale gegevens kunnen tevens zinvol gebruikt worden bij kwantitatieve gegevens. Tussen gegevens gemeten op een intervalschaal en gegevens gemeten op een ratioschaal wordt zelden een onderscheid gemaakt.
2.2 DE DATA MATRIX
Gegevens worden vaak voorgesteld in een matrix waarbij de rijen de elementen van een steekproef voorstellen (bv. individuen, stalen, objecten, …) en de kolommen de verschillende gemeten variabelen (bv. lengte, dikte, aantal eieren, ziek of niet, …). Hoewel er veel verschillende manieren zijn om gegevens in R in te voeren, zullen we in de cursus twee manieren hanteren. Wanneer een dataset relatief klein is, dan kan je rechtstreeks de data invoeren in het script (zie hoger). In andere gevallen is het handiger om eerst een bestand in Excel aan te maken en dan als tab delimited txt bestand op te slaan. Hierbij is het aan te raden om de eerste rij te gebruiken om namen van variabelen in te voeren (zie ook hierboven). Voor je aan de slag gaat, neem de volgende tips of beperkingen in overweging:
- R is case sensitive, bv.. een hoofdletter H is niet hetzelfde als h, zowel in de variabele namen als in karakters
- vermijd dubbel naamgebruik, bv. gebruik verschillende namen voor de dataset en de variabelen
- R gebruikt een punt als decimaal teken, geen komma
- ontbrekende data kan je aangeven met NA, laat geen velden open
Hieronder volgen een aantal manieren om data voor te stellen. Het bevat naast de R-code om de figuren te genereren ook nog een reeks andere functies en tips-and-tricks om data te manipuleren.
2.3 VOORSTELLING VAN UNIVARIATE KWALITATIEVE DATA
Voor een grafische voorstelling van kwalitatieve data wordt vaak gebruik gemaakt van een taartdiagram. Hieronder is zo een plot uitgewerkt in R-code, gebruik makend van de laatst ingevoerde data hierboven:
d<-c(1,2,5,3.5,6,10)
e<-c('eten','drinken','verzekeringen','reizen','auto',
'aankoop vakantiehuis')
pie(d,labels=e)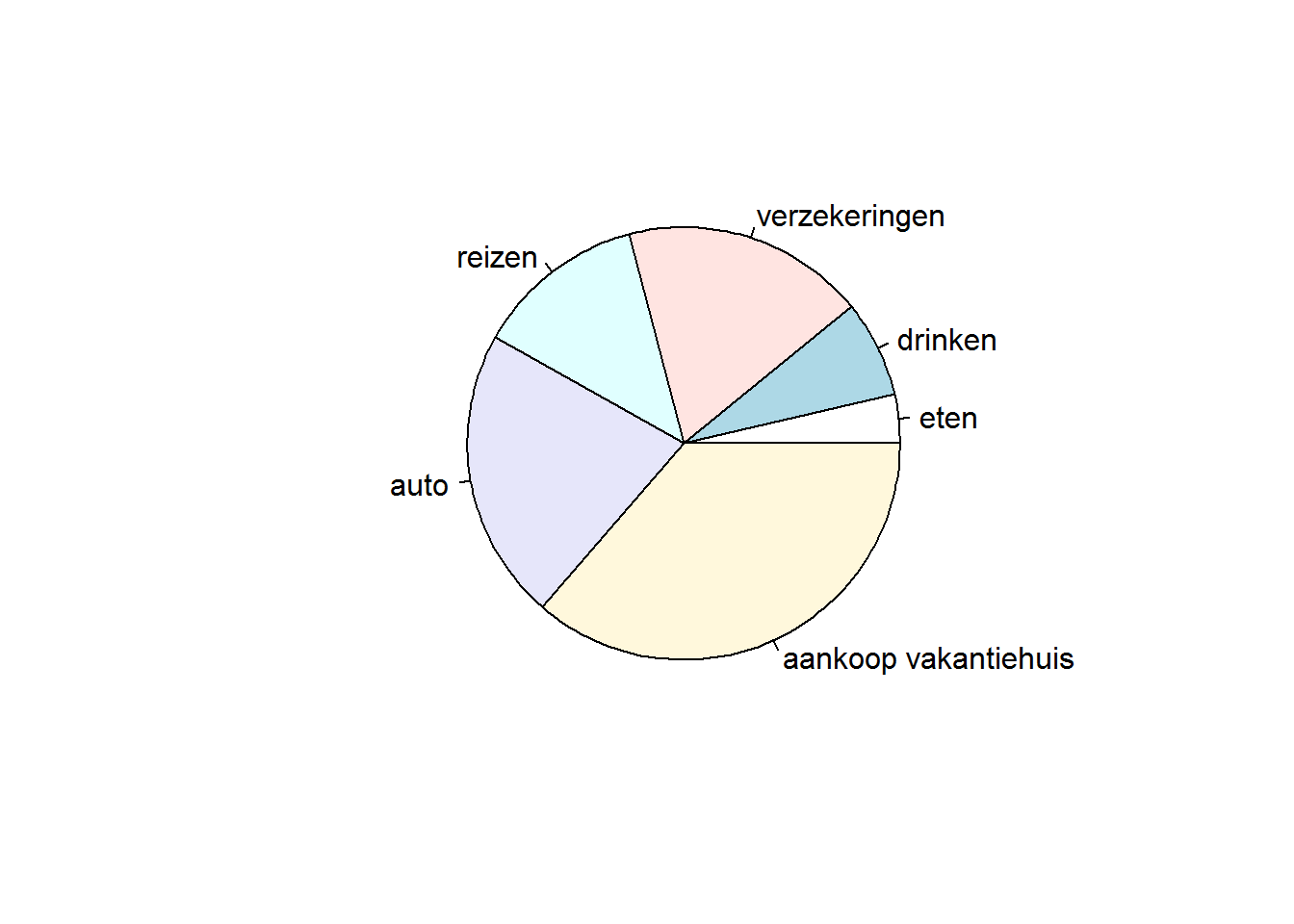
2.4 VOORSTELLING VAN UNIVARIATE KWANTITATIEVE DATA
Kwantitatieve data kunnen op verschillende manieren voorgesteld worden. Elke methode heeft zo zijn voor en nadelen. We zetten de meest gebruikte manieren hieronder even op een rijtje. Hiervoor wordt gebruik gemaakt van een uitgebreide dataset waarin alle medaille winnaars tijdens Olympische spelen in deze eeuw zijn opgelijst per atleet en jaar van deelname. Tevens zijn de leeftijden, sportdiscipline en land van herkomst gekend. Deze data heb ik van het web geplukt, in Excel omgezet tot een txt bestand. Je kunt dat bestand in R opladen met de functie read.table. LET OP, je moet eerst klikken op het file icoontje, en dan op change dir, om te specificeren in welke folder het databestand staat. Het volgende stukje code leest de data in, maakt de inhoud beschikbaar voor de functies die we gaan gebruiken (attach()) en lijst de namen van de variabelen op (names()).
## [1] "Athlete" "Age" "Country" "Year" "Sport" "gold" "silver"
## [8] "bronze"2.4.1 STENGEL-BLAD DIAGRAM
Een van de meest eenvoudige manieren om kwantitatieve data voor te stellen is een stengel-blad diagram. Je kunt het beschouwen als een zijdelings geroteerd histogram, met als toemaatje dat de waarden van alle datapunten ook weergegeven wordt. In onderstaand voorbeeld staat een stukje code om een stengel-blad diagram op te maken. Stel je wilt een stengel-blad diagram maken van de proportie gouden medailles op het totaal aantal medailles per land. Hiervoor moeten we in de dataset eerst het totaal aantal medailles berekenen als de som van goud, zilver en brons. Daarna bereken je het totaal aantal en het totaal aantal gouden medailles per land door gebruik te maken van de tapply functie. De proportie waar een figuur van gemaakt moet worden kan dan berekend worden aan de hand van de twee objecten die de aantallen per land bevatten. Tot slot kan je met de functie stem, het stengel-blad diagram opstellen.
tot<-gold+silver+bronze
land_tot<-tapply(tot,Country,sum)
land_gold<-tapply(gold,Country,sum)
prop<-land_gold/land_tot
stem(prop)##
## The decimal point is 1 digit(s) to the left of the |
##
## 0 | 0000000000000000000000000000000035999
## 1 | 0111345577888
## 2 | 00000123345555666789999
## 3 | 000112233455569
## 4 | 0022345566
## 5 | 00123
## 6 | 0
## 7 |
## 8 |
## 9 |
## 10 | 000000Aangezien we hier met proporties werken zijn alle getallen kleiner dan 1. Op de eerste rij zie je na het | teken 32 nullen staan. Deze komen overeen met 32 keer 0.00, met andere woorden, met 32 landen waarvan de proportie 0 is, en die dus wel medailles behaalden, maar nooit een gouden. Het 33ste getal is 0.03, dus dat is een land waarvan 3% van de behaalde medailles gouden medailles waren. Er zijn ook 6 landen die enkel gouden medailles behaalden. Als je het object prop intikt kan je de ruwe data bekijken en zie je dat Servië het land is met een proportie van 3%. Om na te gaan wie die medaille gewonnen heeft kan je bv. het jaartal, de atleet en de sporttak als volgt zoeken:
## [1] 2012## [1] Milica_Mandic
## 6955 Levels: A._J._Mleczko Aaron_Armstrong Aaron_Egbele ... Zuzana_Štefeceková## [1] Taekwondo
## 49 Levels: Alpine_Skiing Archery Athletics Badminton ... WrestlingEn stel je vast dat in 2012, Milica Mandic als enige Servische atlete een gouden medaille behaalde en dit in Taekwondo.
2.4.2 STAAF DIAGRAM
Een staaf diagram kan gebruikt worden om discrete kwantitatieve data voor te stellen. Zo kan je bv. in R aan de hand van de functie table, tellen hoe vaak een atleet 0, 1, 2, … 8 gouden medailles gewonnen heeft bij een deelname aan de Olympische Spelen:
## gold
## 0 1 2 3 4 6 8
## 5689 2745 150 24 3 1 1Een staaf diagram kan geplot worden met de functie plot. Wat de verschillende opties van een functie inhouden en mogelijk maken kan je terugvinden via de help functie.
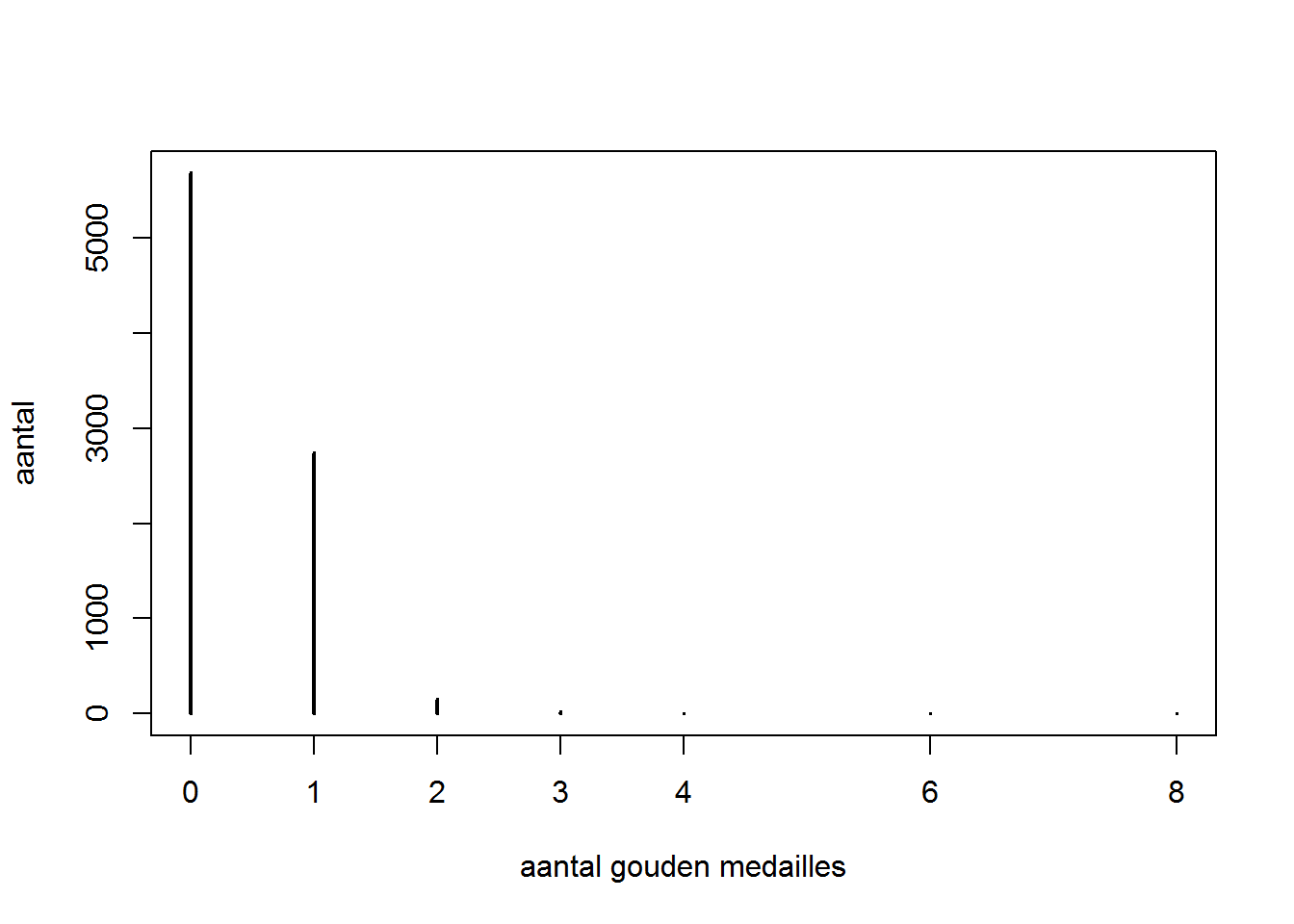
2.4.3 HISTOGRAM
Een histogram kan je vergelijken met een staafdiagram, maar het is toepasbaar op continue data. De continue variabele wordt eerst in klassen ingedeeld, waarna de frequentie van voorkomen voor de verschillende klassen berekend wordt. In R kan je histogrammen maken met de functie hist.
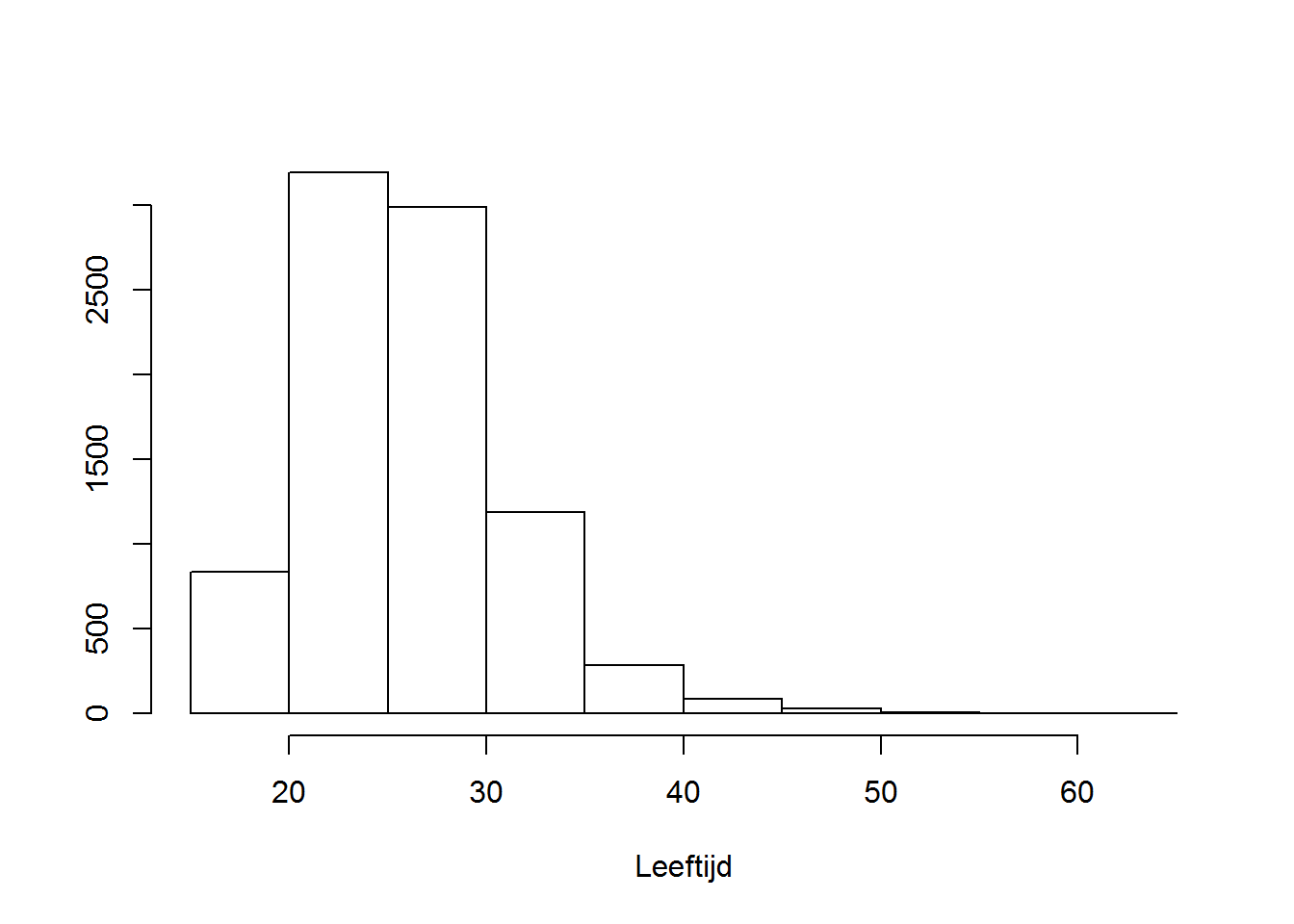
2.4.4 EMPIRISCHE CUMULATIEVE FREQUENTIEVERDELING
Een stengel-blad diagram, staafdiagram en histogram geven een beeld van de frequentieverdeling van je gegevens. Cumulatieve frequentieverdelingen kunnen opgesteld worden voor discrete en continue data en hebben het voordeel dat in een oogopslag kwartielen en de mediaan (zie volgende hoofdstuk) waargenomen kunnen worden. Met behulp van de functie ecdf kan de empirische cumulatieve frequentieverdeling berekend worden waarna ze via de plot functie in een figuur weergegeven kan worden.
emp<-ecdf(Age)
plot(emp,verticals=T,pch='',
main='Cumulatieve frequentieverdeling van leeftijd',
xlab='leeftijd',ylab='')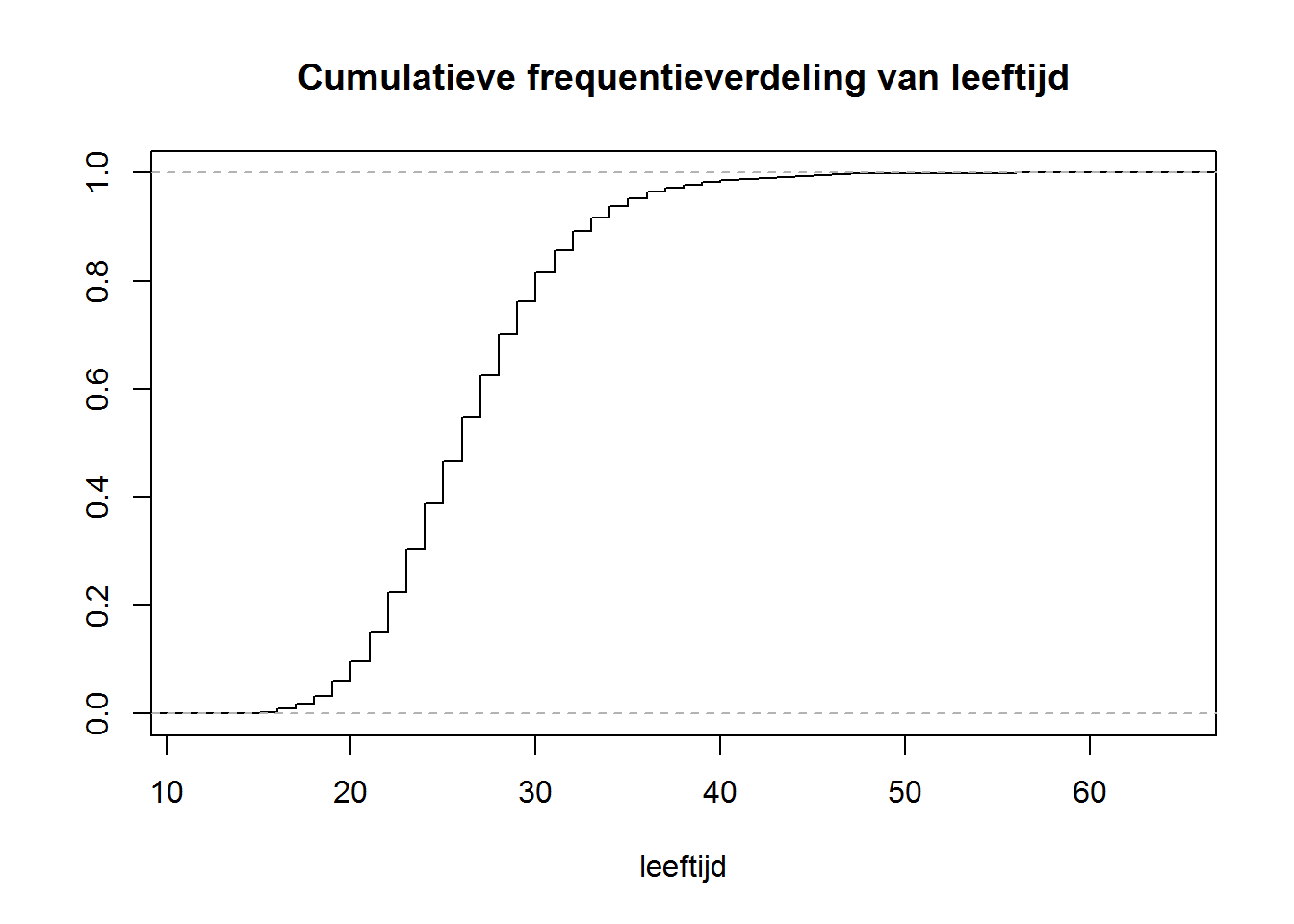
##VOORSTELLING VAN BIVARIATE DATA We bespreken twee manieren om bivariate data grafisch voor te stellen. Stel dat je wilt nagaan in hoeverre er een verband is tussen het behalen van een gouden medaille en leeftijd. Een manier om dit te illustreren is door eerst leeftijden op te splitsen in klassen (dus discreet maken) en dan een kruistabel op te stellen.
## gold
## age2 0 1 2 3 4 6 8
## 10 317 166 17 3 1 1 0
## 20 4009 1918 113 19 2 0 1
## 30 1259 614 19 2 0 0 0
## 40 97 43 1 0 0 0 0
## 50 6 4 0 0 0 0 0
## 60 1 0 0 0 0 0 0Zulke kruistabellen zijn toepasbaar voor alle types van data. De hierboven opgestelde kruistabel bevat erg grote waarden en is moeilijk in een plot te gieten. Laten we daarom voor elke leeftijdscategorie het gemiddelde aantal gouden, zilveren en bronzen medailles berekenen, gebruik makend van de tapply functie.
age_gold<-tapply(gold,age2,mean)
age_silv<-tapply(silver,age2,mean)
age_bron<-tapply(bronze,age2,mean)
med<-rbind(age_gold,age_silv,age_bron)
med## 10 20 30 40 50 60
## age_gold 0.4336634 0.3657209 0.3474129 0.3191489 0.4 0
## age_silv 0.4059406 0.3612669 0.3574446 0.3475177 0.4 1
## age_bron 0.3762376 0.3800726 0.3695882 0.4184397 0.2 0Merk op dat voor de leeftijdsklassen 50 en 60-ers er erg weinig atleten zijn. We gebruiken deze kolommen dan niet om in de plot weer te geven door enkel met de eerste 4 kolommen verder te werken. Een meervoudig staafdiagram kan dan als volgt geconstrueerd worden:
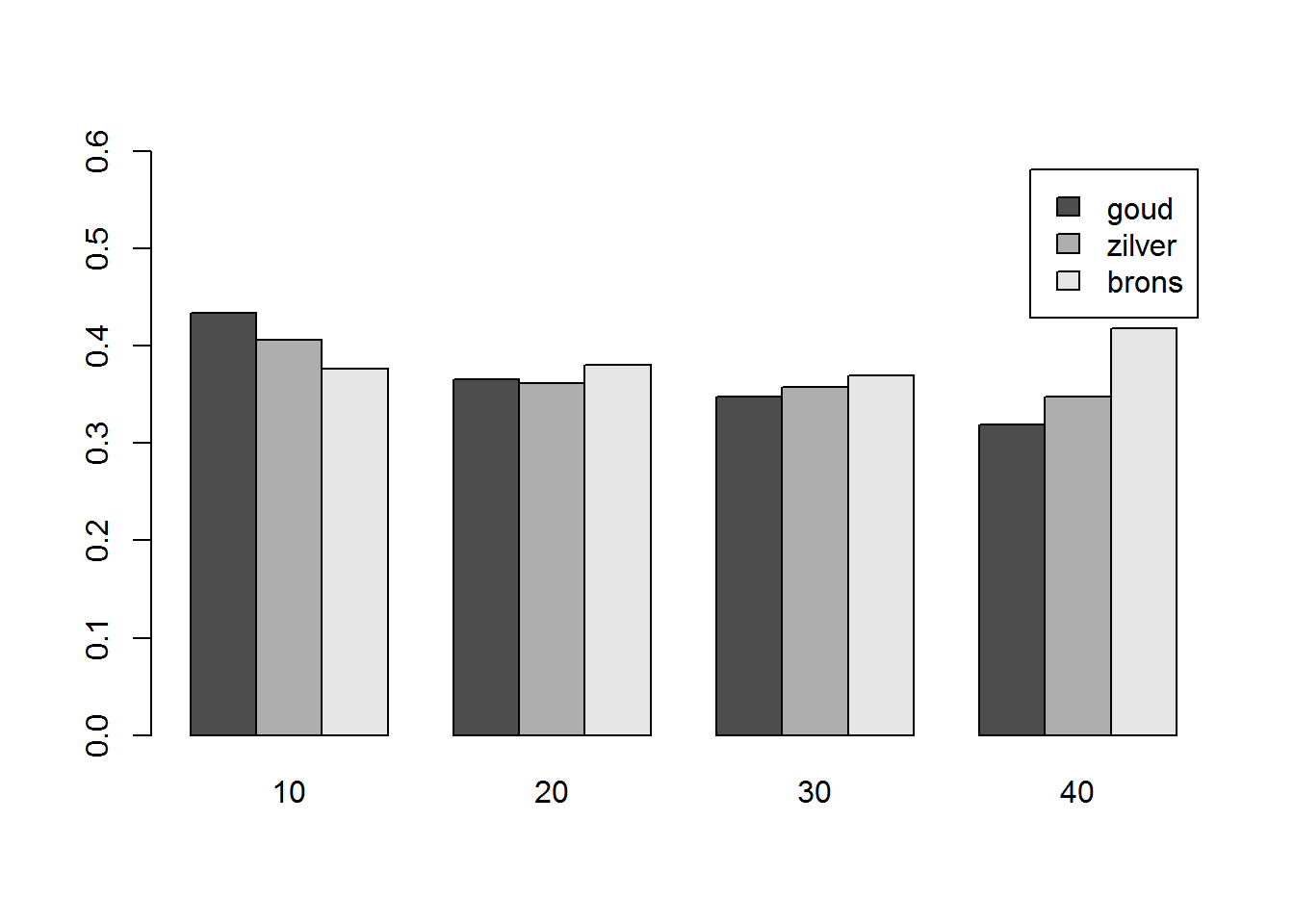
Tot slot, maken we een scatterplot van de gemiddelde leeftijd en jaar van deelname per land, om te bekijken in hoeverre er een associatie is tussen beide.
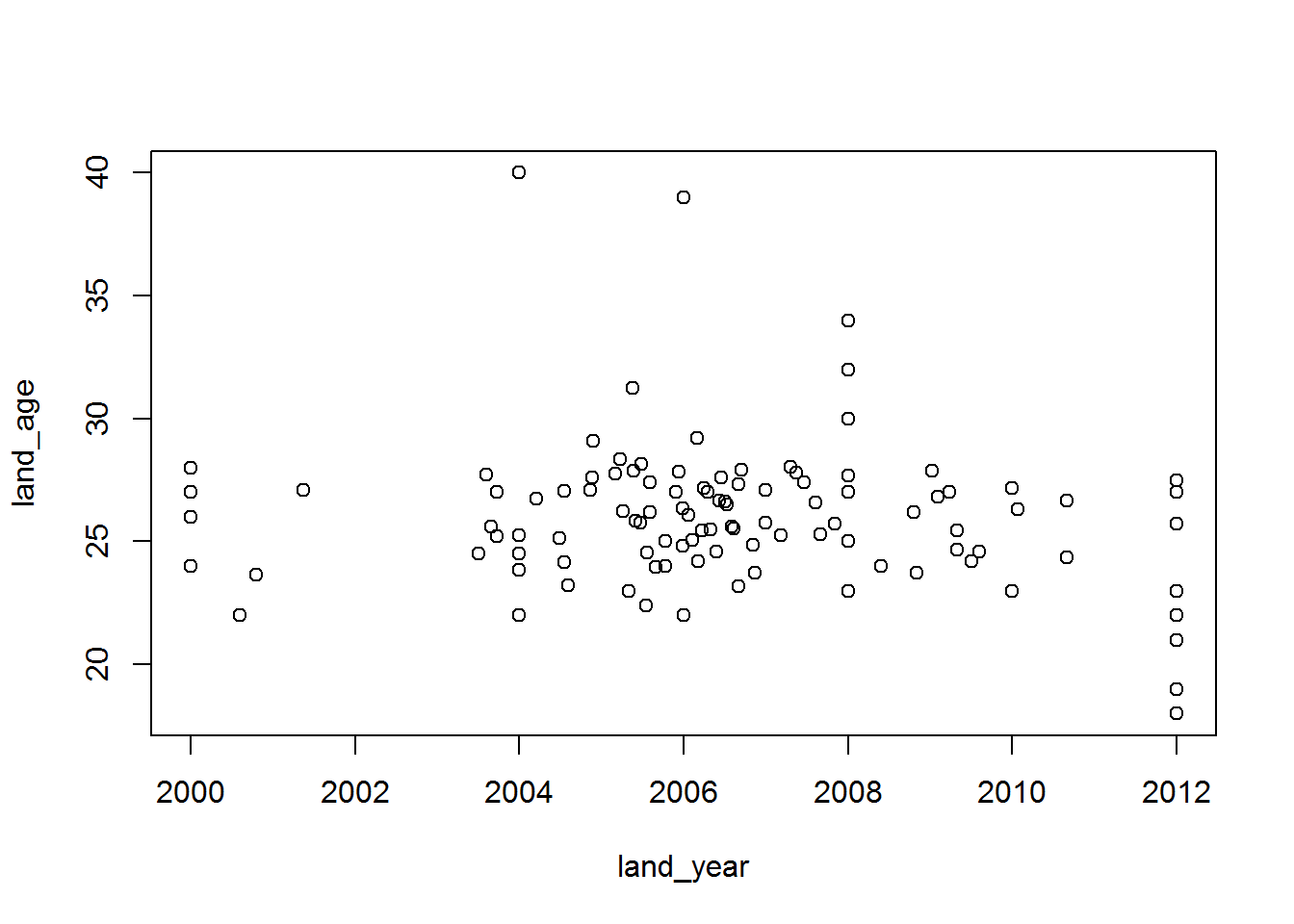
Het is belangrijk dat je de tijd neemt om zelfstandig door de gebruikte codes te gaan en deze bij het oplossen van opdrachten gaat proberen toe te passen tijdens de oefensessies.
2.5 OEFENINGEN
De dataset survey (beschikbaar n het pakket MASS) bevat nominale, ordinale en kwalitatieve data. Je kan de gegevens als volgt oproepen en de achtergrond bekijken:
Maak een stam-blad diagram van ‘Pulse’, een histogram van Age voor de linkshandigen, een kruistabel en meervoudig staafdiagram van Smoke en Exer, een scatterplot van Age en Pulse en een ecdf van de breedte van de schrijfhand. Optioneel: voeg aan deze laatste een ecdf van de niet-schrijfhand toe; tip gebruik de optie add=T en do.points=F in de plot functie.
2.6 DE LUKRAKE STEEKPROEF
In het vorige hoofdstuk werd al aangehaald dat bij statistisch analyses de steekproef de basis vormt en gebruikt zal worden om uitspraken te doen over de populatie. Bij het verzamelen van de steekproef, en eigenlijk al bij de voorbereiding vooraf, moet er met een aantal aspecten rekening gehouden worden. Deze worden hieronder overlopen.
2.6.1 ONAFHANKELIJK
Wanneer een steekproef verzameld wordt, moet ervoor gezorgd worden dat de gegevens onafhankelijk van elkaar zijn. Statistische tests gaan hier in de meeste gevallen van uit. Er bestaan ook technieken die de afhankelijkheid van de data ’in rekening’ kunnen brengen en ervoor corrigeren. In deze cursus zullen we zo twee methodes behandelen (gepaarde t-test en mixed ANOVA modellen. Data zijn afhankelijk van elkaar als je bv. jongen binnen eenzelfde nest opmeet, omdat die een gemeenschappelijk genetische/omgevingsgebonden oorsprong hebben. Ook als je herhaalde metingen neemt op eenzelfde individu dan zijn die data gecorreleerd met elkaar. Wanneer data op verschillende tijdstippen die relatief dicht bij elkaar liggen genomen worden, treedt zgn. temporele autocorrelatie op. Afhankelijkheid kan ook op meer subtiele wijze in de data sluipen. Zo zijn bv. metingen op verschillende herbivore insecten op eenzelfde gastheerplant niet onafhankelijk van elkaar. Tevens kan onder bepaalde omstandigheden verwacht worden dat gastheerplanten die vlak bij elkaar staan meer op elkaar gelijken dan wanneer ze verder van elkaar groeien. Data verzamelt op naburige planten kan ook in zekere maten gecorreleerd zijn en we spreken hier van spatiale autocorrelatie. Een concept dat nauw aan de afhankelijkheid van data gelinkt is staat bekend als pseudoreplicatie. Stel je wilt een experiment uitvoeren waarbij je het effect van een behandeling (bv. lichtregime 100 lux vs. 150 lux) op de groeisnelheid van tomaten wilt bestuderen. Dan kan je een experiment doen door in 1 serre 100 lux en in de andere 150 lux te laten branden en de groei van telkens 50 tomatenplantjes op te meten. Dit is een typisch voorbeeld van pseudoreplicatie, want de verschillende plantjes binnen 1 serre zijn NIET onafhankelijk van elkaar, ze groeien in een gemeenschappelijke omgeving. Het is niet ondenkbaar dat de serres verschillen in nog andere karakteristieken dan de lichtintensiteit. Stel dat serre 1 gemiddeld net een beetje warmer is omdat ze langs de zuidkant staat. Dan gaan alle tomatenplantjes een beetje sneller groeien omdat ze allemaal aan die omgevingskarakteristiek hebben blootgestaan. Je kunt nooit uitsluiten dat er geen andere verschillen zijn dan de lichtintensiteit tussen de twee serres, zodat een schijnbaar ’effect’ van lichtintensiteit (significant verschil in groeisnelheid tussen de twee serres) wel eens te wijten kan zijn aan een andere factor. Dit heet confounding. Een correctere aanpak zou zijn om bv. 10 serres random aan 1 van de 2 behandelingen toe te wijzen en in elke serre een aantal tomatenplantjes op te groeien. De gemiddelde groeisnelheid voor elke van de 10 serres zijn dan wel degelijk onafhankelijk van elkaar. De serres worden dus gerandomiseerd m.b.t. de behandeling. Dit is cruciaal om causale verbanden of effecten aan te tonen. Zogenaamde correlatieve effecten zijn dus niet noodzakelijk causaal omwille van mogelijke confounding met andere factoren die niet gemeten werden. Laat me dit met een (banaal) voorbeeldje illustreren. In Europa is er een verband tussen het aantal ooievaars en het aantal kinderen per gezin. Zoals je wel weet is het niet de ooievaar die de kindjes brengt. De rede voor dit verband is dat van Noord naar Zuid zowel het aantal ooievaars als het aantal kinderen per gezin toenemen. Er is dus confounding tussen het aantal ooievaars en de breedtegraad. De verschillende families werden niet ad random aan de behandeling ’aantal ooievaars’ toegewezen, waardoor we niet in staat zijn om de onderliggende oorzaak van het aantal kinderen per gezin te achterhalen. Bij het concept van onafhankelijkheid is het belangrijk om de vraagstelling in het achterhoofd te houden. Stel dat ik wil testen of mijn bloeddruk verschilt van die van collega X. De populatie waarin ik dan geïnteresseerd ben bestaat uit 2 personen. Om te kunnen inschatten of er een verschil is in bloeddruk hebben we herhaalde metingen nodig van de twee proefpersonen. Het komt er dan op aan om ervoor te zorgen dat de metingen elkaar niet te snel op elkaar volgen. Als ik echter wil toetsen of er een verschil is tussen mannen en vrouwen, dan spreekt het voor zich dat 1 man en 1 vrouw niet voldoende zijn. Bij het nemen van een steekproef moeten tal van beslissingen genomen worden die ervoor zorgen dat de steekproef representatief en niet vertekend is. Wanneer wordt de bloeddruk genomen? Wie komt in aanmerking (leeftijd, ras, type baan, over welke regio)? Deze twee aspecten worden hieronder verder besproken.
2.6.2 REPRESENTATIEF
Bij het nemen van een steekproef is het noodzakelijk om de populatie in het achterhoofd te houden, omdat de steekproef een weerspiegeling moet zijn van de onderliggende populatie die representatief is voor de vraagstelling. Als je bv. uitspraken wilt doen over de boerenzwaluw in West Europa ga je niet enkel in de Kempen een steekproef nemen. Dit concept houdt nauw verband met het bias concept (zie volgende paragraaf).
2.6.3 UNBIASED (NIET VERTEKEND)
Wanneer je een steekproef neemt om een uitspraak te doen over de populatie dan spreekt het voor zich dat die steekproef niet vertekend mag zijn, of in statistische termen: de steekproef moet unbiased zijn. Dat betekent in de eerste plaats dat elke observatie even veel kans moet hebben om in de steekproef terecht te komen. Stel dat je het uitvlieggewicht van koolmeesjongen wilt analyseren, dan moet je ervoor zorgen dat elk jong dat uitvliegt even veel kans heeft om in de steekproef terecht te komen, en dat je niet telkens het eerst uitvliegende jong opmeet. Dit houdt nauw verband met het concept randomisatie dat we eerder al besproken.
Vertekening of bias is een acuut probleem als je bv. met museum stalen moet werken, omdat je kunt verwachten dat soms enkel de mooie, volledige exemplaren verzameld werden. Ook het gebruik van literatuurgegevens kan problematisch zijn, omdat er vaak publication bias optreedt. Statistisch significante resultaten raken nu eenmaal makkelijker gepubliceerd. Bias kan gemakkelijk en op subtiele wijze in je steekproef sluipen. Missing data kunnen ook een belangrijke bron van bias vormen. Vooral bij het bestuderen van natuurlijk populaties gaan een heel deel van de individuen in de loop van de studie verdwijnen door dispersie en/of mortaliteit, en is het vaak niet mogelijk te achterhalen in hoeverre deze een random deel van de studiepopulatie vormen, dan wel dat ze bepaalde eigenschappen bezitten die gerelateerd zijn aan de vraagstelling. Stel dat je wilt nagaan wat het verband is tussen uitvlieggewicht als jong en legselgrootte als volwassene bij koolmezen. Lichtere individuen zijn mogelijk minder dominant en meer genoodzaakt om het gebied te verlaten. Als die individuen die het gebied verlaten en dus niet in je dataset terecht kunnen komen, ook qua legselgrootte verschillen van de individuen die achterblijven, krijg je een vertekend beeld. Dit probleem is ook erg prominent aanwezig in klinische studies. Stel dat je de werking van een experimenteel geneesmiddel wilt testen en dat je patiënten random toewijst aan ofwel een placebo-behandeling (je geeft ze een pilletje maar er zit geen werkend bestanddeel in) of het actieve product. Een eerste potentiële bron van bias is ’patient entry’. In klinische studies is de behandeling gratis, maar vereist veel medische tests en bezoeken aan een arts. Dit kan resulteren in een vertekende groep van patiënten die willen deelnemen aan zo een studie (bijvoorbeeld patiënten waar vorige behandelingen met bestaande geneesmiddelen faalden). Een tweede bron van bias is gerelateerd aan de houding tegenover een experimenteel geneesmiddel. Patiënten kunnen een positieve houding hebben omdat ze weten dat ze een potentieel krachtig geneesmiddel kunnen krijgen of kunnen ook een eerder negatieve houding aannemen uit vrees voor neveneffecten. Als derde bron van bias blijkt dat in zowat elke studie een aantal patiënten verdwijnen, en het is niet ondenkbaar dat het voornamelijk die patiënten zullen zijn waar de behandeling geen effect heeft. Als er dan inderdaad een effect is van het experimentele product dan kan je verwachten dat er een hogere drop out gaat plaatsvinden in de placebogroep. Daarenboven heb je een vertekend beeld van het werkelijke effect van het actieve product omdat er vaak ook een placebo-effect optreedt. De idee een geneesmiddel gekregen te hebben is soms/vaak al een redelijk succesvolle behandeling, en dit is ook buiten het experiment zo. Hierdoor gaan ook de patiënten in de placebogroep een verbetering vertonen, en de patiënten die geen of slechts een beperkt placebo-effect vertonen gaan vaak een grotere kans hebben om de studie te verlaten. Een bijkomend statistisch probleem bij o.a. clinische studies is dat patiënten geselecteerd worden die er relatief slecht aan toe zijn, bv. met erge hoofdpijn. Zelfs zonder behandeling is het dan niet ondenkbaar dat puur door toeval en fluctuaties van de hoofdpijn, gemiddeld gezien de mate van hoofdpijn zal afnemen in deze steekproef. Dit fenomeen wordt regression tot the mean genoemd. Het ligt trouwens aan de basis van de naam van een regressie analyse (zie verder). Het is ook daarom noodzakelijk om een controle groep te onderzoeken en deze verwachte tendens te kunnen inschatten en te vergelijken met een (hopelijk) sterkere verbetering in de groep van behandelde patiënten. Bias sluipt in bijna elk experiment in een of andere vorm binnen, hoe goed het ook ontworpen en uitgevoerd werd. Belangrijk is om, naast bias te minimaliseren, in te zien dat het om elke hoek gluurt en dat je bij de interpretatie van analyses hiermee moet rekening houden.
2.6.4 NAUWKEURIG
Bij de planning van een experiment moet je beslissen hoe nauwkeurig je gaat meten. Dit hangt in grote mate van de vraagstelling af, maar het lijkt in ieder geval zinloos om een olifant tot op 1 mg nauwkeurig te meten terwijl je een koolmees maar tot op 10 gram nauwkeurig zou gaan meten. Een vuistregel die je kunt hanteren is de 30-300 regel. Hiervoor heb je een idee nodig van de range van mogelijke data. Dan tel je het aantal stappen tussen de minimum en maximum waarde en als deze tussen 30 en 300 ligt dan is je accuraatheid voldoende en niet te gedetailleerd. Stel dat koolmezen tussen de 16 en 21g wegen. Dan heb je 5 stappen nodig om van het minimum naar het maximum te gaan als je tot op 1 g nauwkeurig zou meten. Dat is dus onvoldoende nauwkeurig. Bij metingen tot op 0.01 g nauwkeurig zou je 500 stappen nodig hebben wat erop wijst dat dit te nauwkeurige metingen zijn. Als je tot op 0.1 g nauwkeurig meet dan zijn er 50 stappen nodig en dat is volgens deze regel een goede keuze.
2.7 VERSCHILLENDE NIVEAUS VAN ANALYSES
Tot slot kan er een onderscheid gemaakt worden tussen verschillende niveaus waarop statistische analyses kunnen plaatsvinden. In het meest eenvoudige geval spreken we van beschrijvende statistiek, wanneer er enkel op 1 of meerdere manieren een beschrijving van de gegevens uitgevoerd wordt. Dat kan op basis van grafieken (zie hierboven) die dan vaak aangevuld worden met zogenaamde kengetallen (zoals bv. een gemiddelde, zie volgende hoofdstuk). Een stap verder wordt gegaan wanneer hypotheses getoetst worden. Zo ka je je bijvoorbeeld de vraag stellen of het gebruik van een insecticide tot een hogere opbrengst leidt. Enkel met behulp van het berekenen van bv. een gemiddelde opbrengst voor een controle en behandelde groep van planten berekenen is hiervoor onvoldoende (maar wel een zinvolle eerste stap). Daarnaast moet op basis van zgn. statistische tests berekend worden hoe waarschijnlijk het is dat de geobserveerde verschillen ‘echt’ zijn en geen toeval omdat je met steekproeven werkt. Het gebruik van verschillende tests voor verschillende types van hypotheses vormt het grootste deel van deze cursus. Tot slot is het ook mogelijk om op basis van een statistisch analyse, voorspellingen te gaan maken van ongekende waarden. Dit zal toegepast worden in het hoofdstuk regressie.
2.8 OPDRACHTEN LUKRAKE STEEKPROEF
Bespreek van onderstaande voorbeelden het design van het experiment rekening houdend met de 4 criteria die hierboven overlopen werden.
Een bioloog wilt nagaan of er een verschil is in tarsuslengte van kokmeeuwen in Scandinavi¨e en het Iberisch schiereiland. Hij reist naar Stockholm en meet daar de tarsus van 10 meeuwen tot op een halve cm nauwkeurig en doet hetzelfde voor 10 meeuwen in Lissabon.
Om na te gaan wat het effect is van temperatuur (25 vs 28 graden) en CO2 gehalte (hoog vs. laag) op de groei van populieren kweekt een bioloog in totaal 40 populierenplantjes op van eenzelfde kloon. Hij heeft 4 klimaatskasten. In 2 daarvan stelt hij de temperatuur in op 28 graden en houdt hij een hoog CO2 niveau aan. In de twee andere kasten wordt de temperatuur op 25 graden gehouden bij een laag CO2 gehalte.
Een arts wil nagaan wat het effect is van roken op de kans om vroegtijdig te sterven. Hij volgt 200 jongeren, waarvan er 90 roken, gedurende 25 jaar op.
In een studie naar de effecten van inteelt op de legselgrootte van het bont zandoogje wordt uit een labo-populatie 20 broer-zus en 20 random koppels samengeplaatst. Uit elk legsel worden de rupsen opgekweekt en worden random 3 vrouwtjes gekozen. Hun legselgrootte wordt bepaald en vergeleken tussen de twee groepen van koppels.